الإسقاط العمودي على مستو

1. مسقط نقطة على مستوٍ: هو أثر العمود المرسوم من تلك النقطة على المستوي.

2. مسقط مجموعة نقط على مستوي: لتكن $L$ مجموعة من نقاط في الفراغ فإن مسقطها هو مجموع كل آثار الأعمدة المرسومة من نقاطه على المستوي.

3. مسقط قطعة مستقيم غير عمودية على مستوٍ معلوم: هي قطعة المستقيم المحددة بأثري العمودين المرسومين من نهايتي القطعة المستقيمة على المستوي المعلوم.

• ليكن $\overline{AB}$ غير عمودي على $\left(X\right)$
• وليكن $\Leftarrow \overline{AC}\perp \left(\mathrm{X}\right)$ مسقط $A$ على $\left(X\right)$ هو $C$
• $\Leftarrow \overline{BD}\perp \left(\mathrm{X}\right)$ مسقط $B$ على $\left(X\right)$ هو $D$
• مسقط $\overline{AB}$ على $\left(X\right)$ هو $\overline{CD}$

ملاحظة:

إذا كان $\overline{AB}//\left(\mathrm{X}\right)$ فإن $\mathrm{AB}=\mathrm{CD}$

4. المستقيم المائل على مستو: هو المستقيم غير العمودي على المستوي وقاطع له.

5. زاوية الميل: هي الزاوية المحددة بالمائل ومسقطه على المستوي.

• ليكن $\overleftrightarrow{AB}$ مائلاً على $\left(X\right)$ في $B$ ليكن $\overline{AC}\perp \left(\mathrm{X}\right)$ في $C$
• $C\therefore$ مسقط $A$ على $\left(X\right)$ حيث $A\notin \left(\mathrm{X}\right)$
• كذلك $B$ مسقط نفسها حيث $B\in \left(\mathrm{X}\right)$
• $\overline{BC}$ مسقط $\overline{AB}$ على $\left(X\right)$ أي أن $\theta \in (0,{90}^{\circ }),0<\theta <{90}^{\circ }$

6. طول المسقط: طول مسقط قطعة مستقيم على مستوٍ = طول المائل × جيب تمام زاوية الميل فعندما تكون $\overline{AB}$ مائلاً على $\left(X\right)$ وزاوية ميله $\theta$ ومسقطه $\overline{BC}$$BC=AB\cos \theta$

7. مسقط مستوى مائل على $\left(X\right)$: زاوية ميل مستوي على مستوٍ معلوم هو قياس الزاوية المستوية العائدة للزاوية الزوجية بينهما.

مساحة مسقط منطقة مائلة على مستو معلوم = مساحة المنطقة المائلة × جيب تمام زاوية الميل.

لتكن $A$ مساحة المنطقة المائلة، '$A\text{'}$ مساحة المسقط و$\theta$ قياس زاوية الميل $A^{\mathrm{\prime }}=A\cdot \cos \theta$

(1)- إذا وازى أحد ضلعي زاوية قائمة مستوياً معلوماً فإن مسقطي ضلعيها على المستوي متعامدان.

المعطيات:

• $<)ABC$ قائمة في $B$
• $\overline{AB}//\left(\mathrm{X}\right)$
• $\overline{A\text{'}B\text{'}}$ هو مسقط $\overline{AB}$ على $\left(X\right)$
• $\overline{B\text{'}C\text{'}}$ هو مسقط $\overline{BC}$ على $\left(X\right)$

المطلوب إثباته: $\overline{A\text{'}B\text{'}}\perp \overline{B\text{'}C\text{'}}$

البرهان:

• $\overline{A\text{'}B\text{'}}$ مسقط $\overline{AB}$ (معطى).
• $\overline{B\text{'}C\text{'}}$ مسقط $\overline{BC}$ (معطى).
• $\overline{CC\text{'}},\overline{BB\text{'}},\overline{AA\text{'}}\perp \left(X\right)\Leftarrow$
• (مسقط قطعة مستقيم على مستوٍ معلوم هو القطعة المحددة بأثري العمودين المرسومين على المستوي من طرف القطعة المستقيمة).
• $\overline{CC\text{'}}//\overline{BB\text{'}},\overline{AA\text{'}}//\overline{BB\text{'}}$ (المستقيمان العموديان على مستو واحد متوازيان).
• بالمستقيمين المتوازيين $CC\text{'},BB\text{'}$ نعين $\left(\mathrm{Z}\right)$
• بالمستقيمين المتوازيين $AA\text{'},BB\text{'}$ نعين $\left(\mathrm{Y}\right)$
• (لكل مستقيمين متوازيين يوجد مستو وحيد يحتويهما).
• لكن $\overline{AB}//\left(\mathrm{X}\right)$ (معطی).
• $\left(\mathrm{Y}\right)\cap \left(\mathrm{X}\right)=A\text{'}B\text{'}$ (يتقاطع المستويان بخط مستقيم).
• $\overline{AB}//\overline{A\text{'}B\text{'}}⟸$ (إذا وازی مستقيم مستوياً معلوماً فإنه يوازي جميع المستقيمات الناتجة من تقاطع هذا المستوي والمستويات التي تحوي المستقيم).
• كذلك $\overline{BB\text{'}}\perp \overline{A\text{'}B\text{'}}$ (المستقيم العمودي على مستوي يكون عمودياً على جميع المستقيمات المرسومة من أثره ضمن ذلك المستوي).
• $\overline{AB}\perp \overline{BB\text{'}}$ (في المستوى الواحد: المستقيم العمودي على أحد مستقيمين متوازيين يكون عمودياً على الآخر).
• لكن $\overline{AB}\perp \overline{BC}$ (لأن °$m<)ABC={90}^{\circ }$ معطی).
• $\overline{A\text{'}B\text{'}}\perp \left(\mathrm{Z}\right)⟸$ (المستوي العمودي على أحد مستقيمين متوازيين يكون عمودياً على الآخر).
• $\overline{A\text{'}B\text{'}}\perp \overline{B\text{'}C\text{'}}\therefore$ (المستقيم العمودي على مستوي يكون عمودياً على جميع المستقيمات المرسومة من أثره ضمن ذلك المستوي).

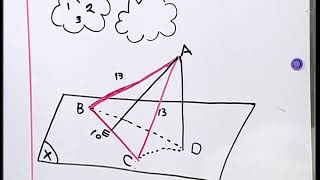
(2)- $ABC$ مثلث، $\overline{BC}\subset \left(\mathrm{X}\right)$ والزاوية الزوجية بين مستوي المثلث $\left(ABC\right)$ والمستوي $\left(X\right)$ قياسها $60°$ فإذا كان $AB=AC=13\mathrm{cm},BC=10\mathrm{cm}$ جد مسقط المثلث $\left(ABC\right)$ على ($\left(X\right)$ ثم جد مساحة مسقط $\mathrm{△}ABC$ على $\left(X\right)$.

المعطيات:

$\mathrm{△}ABC,\overline{BC}\subset \left(\mathrm{X}\right)$

قياس $ABC-\overline{BC}-\left(X\right)={60}^{\circ }$

$BC=10\mathrm{cm},\mathrm{AB}=AC=13\mathrm{cm}$

المطلوب إثباته: إيجاد مسقط $\mathrm{△}ABC$ على $\left(X\right)$ وإيجاد مساحة مسقط $\mathrm{△}ABC$ على $\left(X\right)$.

البرهان: نرسم $\overline{AD}\perp \left(\mathrm{X}\right)$ في $D$ (يمكن رسم عمود على مستوي من نقطة معلومة).

• $\overline{\mathrm{CD}}$ مسقط $\overline{\mathrm{AC}}$
• $\overline{\text{BD}}$ مسقط $\overline{\mathrm{AB}}$
• $\overline{BC}$ مسقط نفسه على $\left(X\right)$
• (مسقط قطعة مستقيم على مستو معلوم هو القطعة المحددة بأثري العمودين المرسومين على المستوى من طريق القطعة المستقيمة).
• $\mathrm{△}BCD\therefore$ مسقط $\mathrm{△}ABC$ على $\left(X\right)$
• في $\left(ABC\right)$ نرسم $\overline{BC}\perp \overline{AE}$ في $E$ (في المستوي الواحد يمكن رسم مستقيم عمود على آخر من نقطة معلومة).
• $AC=AB\because$ (معطی)
• $EC=BE=5\mathrm{cm}\therefore$ (العمود النازل من رأس مثلث متساوي الساقين على القاعدة ينصفها).
• $\overline{ED}\perp \overline{BC}\therefore$ (نتيجة مبرهنة الأعمدة الثلاثة).
• $<)DEA\therefore$ عائدة للزوجية $\overline{BC}$ (تعريف الزاوية العائدة).
• لكن قياس الزاوية الزوجية $\overline{BC}={60}^{\circ }$ (معطی).
• في $\mathrm{△}AEB$ القائم في $E$:
• $AE=\sqrt{169-25}=\sqrt{144}=12\mathrm{cm}$
• في $\mathrm{△}AED$ القائم في $D$:
• $\begin{array}{rl}& \cos {60}^{\circ }=\frac{ED}{AE}\Rightarrow \frac{1}{2}=\frac{ED}{12}\Rightarrow ED=6\mathrm{cm}\\ & BCD \left(\mathrm{المثلث} \mathrm{مساحة}\right)=\frac{1}{2}\times 10\times 6=30{\mathrm{cm}}^2\end{array}$
• (و. هـ. م).

ملاحظة: لو طلب مساحة المسقط فقط فيمكن إيجاده كالآتي:

$\begin{array}{rl}& \cos {60}^{\circ }\times ABC \left(\mathrm{مساحة}\right)=BCD \left(\mathrm{مساحة}\right)\\ & =\frac{1}{2}\times (12\times 10\times \frac{1}{2})=30{\mathrm{cm}}^2\end{array}$

(و. هـ. م).

ملاحظة: كل سؤال يعطي فيه زاوية زوجية علينا اتباع الآتي:

1. معرفة مستقيم تقاطع المستويين الذي هو حرف الزاوية الزوجية.
2. نرسم عمود على حرف الزاوية الزوجية والعمود الآخر نستنتجه من مبرهنة الأعمدة الثلاث.